4 结构参数优化
  4.1 优化模型
  优化问题的数学模型是实际优化设计问题的数学抽象。在大梁优化设计中，明确设计变量、状态变量和目标函数后，大梁优化设计问题可以表示成一般数学规划问题。即：
   

  在满足约束条件向量Y=[y1,y2,…,yn]T的前提下，求设计变量向量X=[x1,x2,…,xn]T使目标函数f(X)=f(x1,x2,…,xn)→min。
   

  1. 设计变量
  大梁、立柱、底梁和支架体组成电除尘器主体承载钢结构,它们在电除尘器中的结构位置受到电除尘器内部电极除尘系统以及其他结构关系的制约,因此在建立优化模型时,主要以梁、柱、支架体板材断面的尺寸和各类型钢的断面尺寸作为设计变量，经过筛选和组合，选定26个设计变量组成设计变量向量X=[x1,x2,…,x26]T。
   

  2. 约束条件
  包括几何约束和性能约束：
  几何约束主要根据刚架结构的设计、制造、工艺和装配等要求，对设计变量的上下界进行控制。
   

  对于性能约束，应设计单位要求，对优化控制进行强度和刚度约束，刚度约束保证结构和材料合理变形，强度约束根据第四强度理论进行约束。
   

  3. 目标函数
  将结构重量作为目标函数f(X)，显然，f(X)是设计变量X=[x1,x2,…,x26]T的函数。
   

  4.2 优化方法
  ANSYS程序提供了两种优化的方法，本文选用First-Order一阶方法。
  强度和几何约束使电除尘器结构优化成为约束优化问题。First-Order方法通过对目标函数添加罚函数将问题转换为非约束问题。
   

  该方法基于目标函数对设计变量的敏感程度，使用因变量对设计变量的偏导数进行分析，在每次迭代中，用最大斜度法或共轭方向法确定搜索方向，并用线搜索法对非约束问题进行最小化。因此，每次迭代都有一系列的子迭代（其中包括搜索方向和梯度计算）组成，这就使得一次优化迭代有多次分析循环，耗用计算机时较多，但结果非常精确。
   

  First-Order方法在目标函数值由非常好的合理设计到当前设计的变化小于目标函数允差或者从当前设计到前面设计目标函数的变化值小于允差时收敛或中断。
   

  First-Order方法计算实际有限元解（而非逼近），在计算过程中会根据给定的目标函数允差找到确切的结果。因为模型重量72吨多，非常好的合理设计到当前设计的重量变化小于一定值时再继续迭代将不再有多大实际意义，因此，为防止目标函数允差过紧引起迭代次数过多，本文目标函数允差设为10kg，迭代将在非常好的合理设计到当前设计的变化小于10kg时结束。 
   

  4.3 参数化程序
  图2虚拟样机采用ANSYS参数化设计语言APDL建模，优化程序在此基础上定义参数指出设计变量，状态变量和目标函数。所建立的优化程序（包含样机参数化模型）可以很容易的实现该型号电除尘器空间结构几何建模、强度仿真和虚拟样机优化设计，优化部分略作修改可以很方便的移植到其他优化设计问题中，可重用性和通用性良好。
  APDL优化程序（略）。
   

  4.4 结果分析

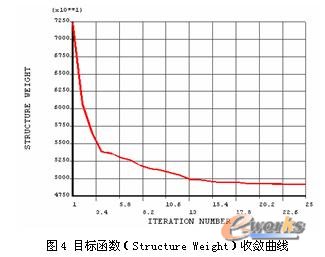
  优化迭代25次(设计序列略)，目标函数收敛曲线如图4所示。模型原重量72344.1090kg，优化后重49239.3500kg，相对于模型重量，减轻23104.7590kg，目标函数下降31.94%；基于材料和制造方面的考虑，对设计变量结果进行适当修正，修正后重量53645.6848kg 相对于模型重量，减轻18698.4242kg，目标函数下降25.85%。设计变量优化结果和修正值（略）。