1 前言
随着物质生活水平的提高,生活方式的改变,心血管疾病发病率越来越高,由于心血管狭窄引起的冠心病已经成为危及人类生命健康安全的主要疾病之一。目前,冠心病的治疗分为药物治疗、外科手术和介入治疗三大类。药物治疗周期长、见效慢、副作用大,患者容易产生对药物的依赖性;外科手术会对病人产生永久性的伤害;介入性治疗方法因其创伤小、效果好,成为目前治疗心血管狭窄的新型方法。
一个完整的支架扩张过程包括支架压握收缩、支架自由扩张和支架与狭窄血管接触后共同扩张三个连续阶段,该过程如图1所示。支架扩张植入过程是临床上支架植入手术能否成功的关键,也是考验支架扩张性能能否满足使用要求的关键阶段,因此该阶段是国内外研究的热点。
Lally等人[1]研究了美敦力S7支架和波士顿NIR支架在扩张变形过程中与血管的相互作用;Walke等人[2]采用有限元分析和实验相结合的方式研究了支架于血管内扩张的生物力学特性;Zhou等人[3]研究动脉支架结构的稳定性及其扩张时的动态成形特点;Chua等人[4-5]研究了扩张过程中球囊和支架之间的相互作用,以及不同加载速度对支架扩张性能、短缩量和最后应力分布的影响;Migliavacca等人[6-8]利用有限元法预测了冠脉支架的力学行为,研究了多种不同结构的支架在不同金属覆盖率的情况下的扩张压力和翘曲量,以及支架波形环之间的链接形式对支架柔韧性的影响;Auriccchio等人[9]重点研究了球囊扩张支架与狭窄血管之间相互作用的生物力学特性;Dumoulin等人[10]分析评价了P308 Palmaz支架的扩张性能及其长期效果。
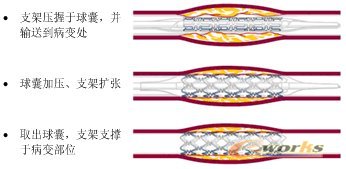
图1 支架植入过程示意图
然而,完整的支架扩张过程包括支架植入前的压握收缩、支架自由扩张、支架与血管狭窄处接触后扩张三个阶段,上述研究工作都未将支架压握收缩纳入到支架扩张过程中,缺少完整考虑支架扩张过程,以及将球囊、支架和血管三者相耦合的研究工作。同时由于支架扩张变形过程是一个同时具有几何非线性和边界条件非线性(接触)的高度非线性问题,针对这样一个弹塑性大变形的问题,支架扩张过程变形机理研究还不够深入。
因此,本文提出对球囊扩张式血管支架耦合扩张过程数值模拟方法进行研究的思想,将支架扩张基础理论研究和支架研制测试相结合,通过建立支架耦合扩张变形有限元模型,深入研究其扩张变形机理;同时,通过实验测试作为对支架耦合扩张数值模拟的补充和合理性的验证,为支架的优化设计及其扩张过程的有限元模拟提供有力的支持。
2 Pro/E-ANSYS-DYNA联合建模求解技术
鉴于支架扩张变形过程是一个同时具有几何非线性、材料非线性(或称物理非线性)、边界条件非线性(接触)的高度非线性问题,针对支架在球囊压力作用下发生的大变形弹塑性接触耦合扩张过程,可以采用隐式算法和显式算法两种方法求解。隐式算法是将时间变量离散化,求解离散时刻的数值解,通过变形体整体平衡方程建立以位移为变量的方程组,用数值求解方法求解不同时刻的位移场。如果采用隐式算法求解支架耦合扩张,由于接触状态复杂,经常会遇到迭代收敛困难问题。动力显式算法是利用动力学控制方程和显式中心差分法直接计算各个时刻的位移场,不涉及方程组求解问题,不用考虑收敛问题,适合于大规模高度非线性的接触分析问题,近年来已经成为高度非线性分析中较流行的方法。因此,本文将支架扩张视为一种准静态的大变形弹塑性接触耦合扩张过程,采用动力显式算法对支架耦合扩张变形过程进行动力学求解。
LSTC(Livermore Software Technology Corporation)公司的DYNA软件作为世界上最著名的通用动力显式分析程序,能够模拟真实世界的各种复杂问题,特别适合求解各种二维、三维非线性结构的高速碰撞、爆炸和金属成形等非线性动力冲击问题,同时可以求解传热、流体及流固耦合问题。从理论和算法而言,LS-DYNA是目前所有的显式求解程序的鼻祖和理论基础,在工程应用如汽车安全设计、武器系统设计、金属成形、跌落仿真等领域被广泛认可为非常好的的分析软件包。目前,LS-DYNA最新版本970版是功能齐全的几何非线性(大位移、大转动和大应变)、材料非线性(140多种材料动态模型)和接触非线性(50多种接触模式)程序,以Lagrange算法和结构非线性动力显式分析为主,是军用和民用相结合的通用结构分析非线性有限元程序。
鉴于以上LS-DYNA在处理几何、材料和接触非线性的杰出能力,本文采用了LS-DYNA作为支架耦合扩张动力显式分析的求解器。同时,考虑到支架网孔结构的复杂性,以及ANSYS强大的前处理功能,采用了Pro/E-ANSYS-DYNA联合建模求解技术,求解流程如图2所示。
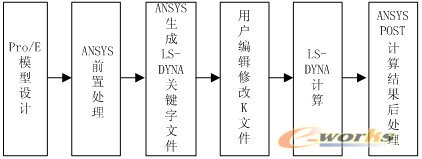
图2 Pro/E-ANSYS-DYNA联合建模求解技术流程图
本文用于有限元分析的球囊、支架和狭窄血管的装配体模型来源于Pro/E设计。通过ANSYS与Pro/E之间的接口或者IGES格式,可以将Pro/E模型完整、顺利地导入到ANSYS中。由ANSYS进行支架耦合扩张的有限元前置处理之后,将支架耦合扩张模型输出成LS-DYNA需要的关键字输入文件(文本格式)。由于目前ANSYS对LS-DYNA的支持并不完善,LS-DYNA中的一些功能并不能从ANSYS的GUI操作或显式命令中得到,因此还需要对关键字文件进行修改、增加或删除部分控制参数语句后,然后再交由LS-DYNA计算程序进行动力显式计算。计算结束后,采用ANSYS/POST进行后处理。
3 支架扩张过程数值模拟的关键技术
3.1支架、球囊和血管的耦合模型
将支架、狭窄血管和球囊各部件分别建模后,装配成三维实体模型。在进行支架耦合扩张分析时,利用装配模型几何形状的对称性,使用装配模型的八分之一进行扩张模拟,即取周向的四分之一和轴向的二分之一后得到,简化后的八分之一模型如图3所示,在耦合模型中部垂直于支架轴向做一剖面,该断面如图4所示,该耦合模型参数值见表1所示。
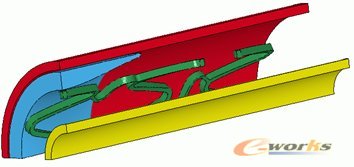
图3 支架、狭窄血管和球囊耦合简化模型
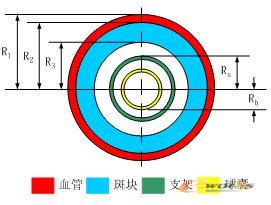
图4 耦合模型截面
表1 耦合模型参数值(单位:mm)
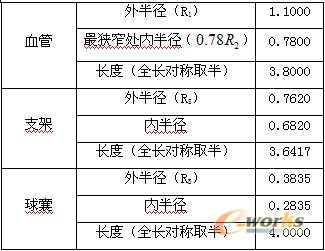
3.2材料模型选取
对于支架本体采用双线性等向强化弹塑性模型描述奥氏体316L医用不锈钢支架的材料;分析用球囊采用Johnson公司2.0mm规格的RAPTORRAIL球囊,其材料为聚亚安酯。对于血管的材料模型,将血管看成各向同性的弹性管,但是狭窄血管的弹性模型与泊松比根据国外最新研究成果[4]选取。综上所述,将支架、球囊和血管的材料模型汇总,如表2所示。
表2材料模型
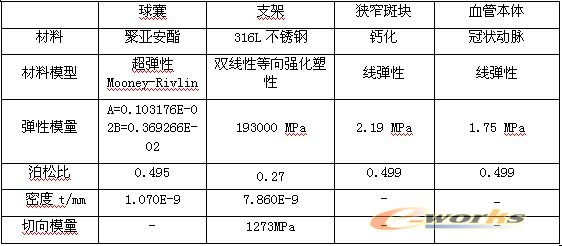
3.3网格划分方法
由于球囊和血管本体的结构比较简单规则,故采用8节点六面体单元进行均匀的映射网格划分;由于支架结构复杂,适合采用10节点的四面体单元划分网格,考虑到支架波形环及其连接杆附近将是大变形的集中区域,因此在这些区域进行了网格细化;对于狭窄斑块,由于其表面不规则,而且斑块会在支架的挤压作用下发生大变形,为避免单元畸变而出现负体积问题而使计算终止,采用较密的10节点的四面体单元划分网格,整个耦合模型划分网格后如图5所示,其单元与节点详情如表3所示。
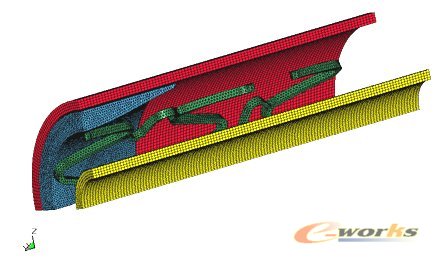
图5 划分网格后的耦合模型
表3 节点与单元
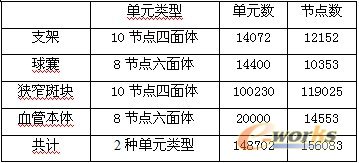
3.4边界条件
在对支架施加约束条件时,必须确保支架在发生大变形扩张整个过程中都是适合的,合理的约束条件是支架扩张变形模拟的关键之一。在建模时选笛卡儿坐标系的y轴为支架轴心,则支架的约束条件为:对支架上平行于yz平面和xy平面的所有节点施加对称约束,即位于该对称约束平面上的节点只能在该平面内运动,而不能沿垂直于该平面的方向运动;对支架轴向中心处的所有节点施加轴向y方向约束,即支架中心处所有节点只能沿径向运动,不能沿轴向y方向运动,而支架末端不施加约束,可沿径向和轴向自由伸缩,约束条件如图6所示。球囊和狭窄血管的约束条件与支架类似,有一点不同就是除在其对称面施加对称约束外,需要将球囊和血管本体的末端完全固定。
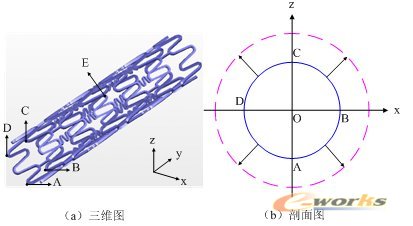
图6 约束条件
3.5载荷定义
载荷的施加采用增量方法,载荷作用时间如图7分为四个阶段。0~t2时间段为支架压握收缩阶段,对支架外表面施加均匀分布压力,该压力从0逐渐增加到t1时刻的最大值P1,P1为支架恰好收缩到内径与球囊外径相等时的压力,在t2时刻该压力释放为0;t2~t3时间段为支架扩张阶段,此时对球囊内表面施加均匀分布压力,该压力从0逐渐增加到最大值P2,P2为支架扩张到预定外径时的压力;t3~t4时间段为压力保持阶段,当支架扩张到预定外径后,维持此时压力P2一段时间;t4~t5时间段为压力卸载阶段,此时球囊内表面施加压力从最大值P2减小到0,用以模拟球囊泄压过程。可见,从0~t5中所施加的载荷已经模拟出支架压握、扩张和释放整个过程,有限元分析结果也证明该载荷施加方法是恰当的。
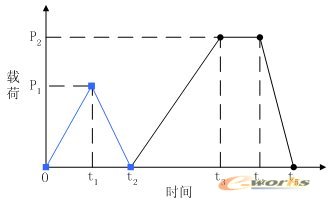
图7 载荷变化曲线
3.6支架扩张数值模拟接触非线性处理
在球囊与支架以及支架与血管壁接触过程中,彼此间作用的载荷随时间和结构变形而变化,也即结构与载荷互相耦合。本文选用基于罚函数的面-面接触算法来处理球囊外表面与支架内表面、支架外表面与狭窄血管内壁的非线性接触问题,建立球囊与支架,以及支架与狭窄血管两个接触对。对于球囊与支架接触对,球囊为目标面,支架为接触面;对于支架与狭窄血管接触对,支架为主动接触面,狭小血管硬化斑块为被动接触面。假设支架和狭小血管硬化斑块接触过程中,二者之间没有滑动,因此可以取支架和狭小血管硬化斑块之间的摩擦系数为0。接触刚度的定义是接触算法中的关键问题,所有的接触问题都需要定义接触刚度,两个表面之间渗透量的大小取决了接触刚度。通常有限元程序会根据变形体单元的材料特性来估计一个缺省的接触刚度值,用户也可以为接触刚度指定一个比例因子或指定一个真正的值,比例因子一般在0.01和10之间,选取原则一般是在选取足够大的接触刚度的同时,应该尽量使渗透到达极小值。为了取得一个较好的接触刚度值,开始时取一个较低的值,然后根据计算结果逐步增加接触刚度值,直到结果满意为止。
3.7计算精度与球囊加压速度分析
在ANSYS/LS-DYNA动力显式算法中,影响计算精度的因素很多,主要包括支架、球囊和血管的几何模型描述、耦合模型的有限元单元划分、耦合模型各组成的材料模型选择、支架耦合变形中的接触形式、虚拟球囊加压速度等。在动力学系统中,外力所作的功等于系统的内能、动能、沙漏能、弹性能与阻尼能以及摩擦能之和。在支架扩张动态仿真过程中,由于球囊加压速度的提高,系统动能会明显上升,这势必影响整个系统的能量分配,并加剧材料单元的沙漏变形,从而影响仿真计算的精度。
采用动力显式算法模拟支架耦合扩张变形这类准静态过程时,提高虚拟球囊加压速度有利于提高计算效率,为保证计算精度,提高虚拟球囊加压速度应同时满足以下两个准则:①动能与内能的比值<5%;②沙漏能与内能的比值<5%。作者将仿真计算结果与实验数据进行比较,验证了该准则的合理性,并将该准则用于本文的支架耦合扩张变形动态仿真分析中,支架耦合扩张动力显式分析的系统能量变化曲线如图8所示。
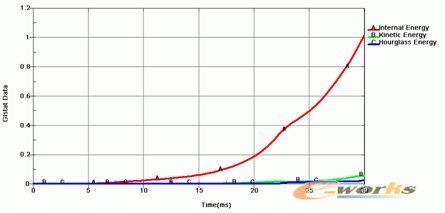
图8 支架耦合扩张动力显式分析的系统能量
4 支架扩张过程仿真结果分析
在施加如图7所示的载荷后,支架耦合扩张整个过程的变形结果如图9所示。为将支架整个耦合扩张过程变形结果介绍清晰,将其分为三个阶段:压握阶段(0~t2)、加压与压力保持阶段(t2~t4)和压力释放阶段(t4~t5)。需要指出的是,在分析计算时采用的是简化后的八分之一模型,为了更真实地查看模型变形结果,采用了后处理软件的模型映射功能,从而将八分之一模型还原为完整模型进行显示。
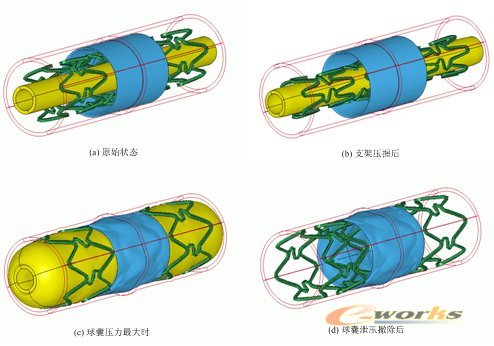
图9 支架耦合扩张过程变形结果(血管本体显示为线框图)
为便于比较,将支架扩张各阶段的变形结果以及计算得到的比率值分别见表3和表4。
表4支架变形结果(单位mm)
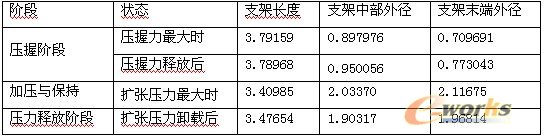
表5计算得到的比率值
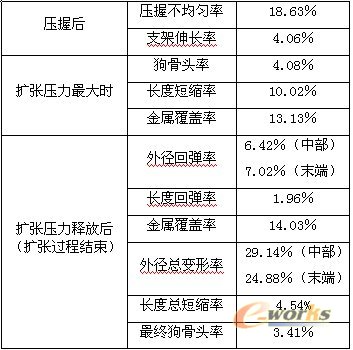
通过这些计算结果,可以看出我们设计的新型支架结构是合理的,它沿径向的扩张比较均匀,其外径和长度变化在我们预期的范围内,而且其金属覆盖率、径向抵抗力和柔韧度等指标都是令人满意的。
5 实验结果分析
为了验证数字模拟的准确性,建立了基于机器视觉技术的支架体外扩张测试平台,并将加工的实物支架在所建立的测试平台上进行了多次实物扩张实验,图10显示了支架扩张过程中不同阶段的变形情况,下面对实验测试结果与有限元分析结果做对比分析。
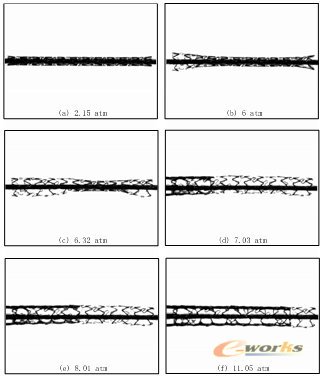
图10 扩张过程中采集到的支架实物形状
从图10中我们发现,在支架外径随扩张压力增加而变化的过程中,支架末端外径的扩张速度明显快于支架中部外径,造成这一现象的原因是实验所用的球囊超过支架的长度较大造成的。由于在进行支架实物扩张时是从支架压握状态开始的,因此这里主要针对支架耦合扩张有限元分析中的支架中部外径随扩张压力增加时的变化规律与实验测试结果做详细讨论。这里将实验测试结果得到的支架中部外径随扩张压力增加时的变化曲线与相应的有限元分析结果,绘制到同一图表以便于观察,如图11所示。
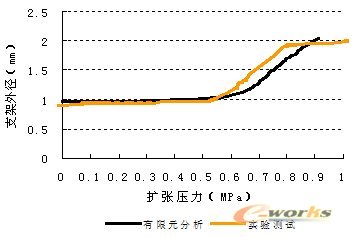
图11 有限元分析与实验测试的支架外径随压力增加时的变化
图11表明支架外径随扩张压力增加时的实验测试结果与相应的有限元分析结果的变化趋势是一致的,实验测试时支架外径的变化速度要快于有限元分析结果,即分别使支架扩张到相同外径时实验测试时所需要的扩张压力要小于有限元分析时所需要的压力,造成这一现象的原因是加工出支架实物时,需要经过清洗抛光等工序,这些工序都会减少支架壁厚和波形环宽度等几何参数,使支架刚度有一定程度的降低,从而使支架变得容易变形;还可以看到,实验测验时当支架外径达到一定值时,再继续增加球囊压力的时候支架外径的变化很小,近似表现为一条平缓的直线,这是由球囊特性决定的,一般情况下球囊在其名义(规格)尺寸附近都会表现出低顺应性的特点,例如强生公司2.0mm的RAPTORRAIL球囊的顺应曲线,当球囊外径在2.0mm附近时,球囊扩张压力在2~10大气压增加时,却仅仅能引起球囊外径的变化范围为1.86~2.14mm。
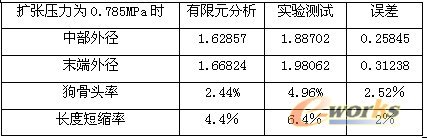
为进一步量化有限元分析结果与实验测试结果的近似程度,选取实验测试时外径从迅速扩张到趋于变化平缓时的转折时刻的扩张压力为参考点(即扩张压力为0.785MPa),计算此时支架变形对比结果见表5。
表6有限元分析结果与实验结果对比(单位:mm)
6 结论
由表5可见,实物支架在扩张时整体变形量要比有限元模拟结果大,在外径变形上二者的误差约为15%,这个误差对于大变形弹塑性有限元计算来说是比较合理的,出现误差的原因有数值计算误差、线性强化大变形弹塑性模型、耦合接触传递误差、支架加工误差以及实验中支架扩张的不均匀性等等。从整个实验台使用效果来看,基于机器视觉技术的测量方案是适合而且满足支架体外扩张实验的。同时,也从一定程度上证明本文采用的ANSYS/LS-DYNA动力显式数值模拟方法是适合用于支架耦合扩张分析的,而且也说明建立的支架耦合扩张有限元模型是合理的。(e-works)
致谢
感谢东南大学易红校长和倪中华老师的指导;感谢航天一院18所研发中心黄玉平主任的支持。
[参考文献]
[1] Lally C, Dolan F, Prendergast P J. Cardiovascular Stent Design and Vessel Stresses:A Finite Element Analysis [J]. Journal of Biomechanics, 2005, 38: 1574-1581.
[2] Walke W, Paszenda Z, Filipiak J. Experimental Andnumerical Biomechanical Analysis of Vascular Stent [J]. Journal of Materials Processing Technology, 2005, 164-165: 1263-1268.
[3] Zhou C T, Dong H Y. Stability and Dynamic Deforming Process for Structure of Coronary Artery Stents [J]. Current Applied Physics, 2005, 5: 458-462.
[4] Chua S N D, Macdonald B J, Hashmi M S J. Finite-Element Simulation of Slotted Tube (Stent) with the Presence of Plague and Artery by Balloon Expansion [J]. Materials Processing Technology, 2004, 155-156: 1772-1779.
[5] Chua S N D, Macdonald B J, Hashmi M S J. Effects of Varying Slotted Tube (Stent) Geometry on Its Expansion Behaviour Using Finite Element Method [J]. Materials Processing Technology, 2004, 155-156: 1764-1771.
[6] Migliavacca F, Petrini L, Montanari V, et al. A Predictive Study of the Mechanical Behaviour of Coronary Stents by Computer Modeling [J]. Medical Engineering & Physics, 2005, 27: 13-18.
[7] Migliavacca F, Petrini L, Colombo M. Mechanical Behavior of Coronary Stents Investigated through the Finite Element Method [J]. Journal of Biomechanics, 2002, 35: 803-811.
[8] Petrini L, Migliavacca F, Auricchio F, et al. Numerical Investigation of the Intravascular Coronary Stent Flexibility [J]. Journal of Biomechanics, 2004, 4: 495-501.
[9] Auriccchio F, Loreto M D, Sacco E. Finite-Element Analysis of a Stenotic Artery Revascularization through a Stent Insertion [J]. Computer Methods in Biomechanics and Biomedical Engineering, 2000, 00: 1-15.
[10] Dumoulin C, Cochelin B. Mechanical Behaviour Modelling of Balloon-Expandable Stents [J]. Journal of Biomechanics, 2000, 33: 1461-1470.


